RATE/VELOCITY OF CHEMICAL REACTION:

Rate $=\frac{\Delta \mathrm{c}}{\Delta \mathrm{t}}=\frac{\mathrm{mol} / \text { lit. }}{\mathrm{sec}}=\mathrm{mol} \mathrm{lit}^{-1}$ time $^{-1}=\mathrm{mol} \mathrm{dm}^{-3}$ time $^{-1}$

Types of Rates of chemical reaction :

For a reaction $\mathrm{R} \longrightarrow \mathrm{P}$

Average rate $=\frac{\text { Total } \text { change in concentration }}{\text { Total time taken }}$

$\mathrm{R}_{\text {instantaneous }}=\lim _{\mathrm{t} \rightarrow 0}\left[\frac{\Delta \mathrm{c}}{\Delta \mathrm{t}}\right]=\frac{\mathrm{dc}}{\mathrm{dt}}=-\frac{\mathrm{d}[\mathrm{R}]}{\mathrm{dt}}=\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{dt}}$

RATE LAW (DEPENDENCE OF RATE ON CONCENTRATION OF REACTANTS):

Rate $=K$ $(conc.)^{\text {order }}$ - differential rate equation or rate expression

Where $\mathrm{K}=$ Rate constant = specific reaction rate $=$ rate of reaction when concentration is unity

unit of $\mathrm{K}=(\text { conc })^{1-\text { order }}$ time $^{-1}$

Order of reaction:

$m_{1}A + m_{2}B \longrightarrow$ products

$R \propto[A]^{p}[B]^{q} \quad$ Where $p$ may or may not be equal to $m_{1}$ & similarly $q$ may or may not be equal to $m_{2}$.

$p$ is order of reaction with respect to reactant $A$ and $q$ is order of reaction with respect to reactant $B$ and $(p+q)$ is overall order of the reaction.

INTEGRATED RATE LAWS:

$C_0 \text{ or ‘a’ is initial concentration and } C_1 \text{ or (a - x ) }\text { is concentration at time} ’t’$

(a) zero order reactions:

$\quad\quad$ Rate $=\mathrm{k}[\text { conc. }]^{0}=$ constant

$\quad\quad$ Rate $= k = \frac{C_0 - C_1}{’t’}\quad or \quad C_1= C_0-kt$

$\quad\quad$ Unit of $K=\mathrm{mol} \quad \mathrm{lit}^{-1} \mathrm{sec}^{-1}$, Time for completion $=\frac{\mathrm{C}_{0}}{\mathrm{k}}$

$\quad\quad$ at $t_{1 / 2}, C_{t}=\frac{C_{0}}{2}, \quad so \quad kt_{1 / 2}=\frac{C_{0}}{2}$

$\quad\quad$ $\rightarrow t_{1 / 2}=\frac{C_{0}}{2k} \quad \therefore t_{1 / 2} \propto C_{0}$

(b) First Order Reactions:

$\quad\quad$ (i) Let a $1^{\text {st }}$ order reaction is, $A \longrightarrow$ Products

$\quad\quad$ $t=\frac{2.303}{k} \log \frac{a}{a-x} \quad$ or $\quad k=\frac{2.303}{t} \log \frac{C_{0}}{C_{t}}$

$\quad\quad$ $\Rightarrow \quad \mathrm{t}_{1 / 2}=\frac{\ell \mathrm{n} 2}{\mathbf{k}}=\frac{0.693}{\mathbf{k}}=$ Independent of initial concentration.

$\quad\quad$ $t_{Avg.} = \frac{1}{k} = 1.44\quad t_{1/2}.$

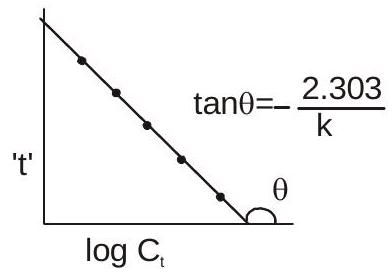
Graphical Representation:

$t=-\frac{2.303}{k} \log C_{t}+\frac{2.303}{k} \log C_{0}$

or $\log a / a-x$

(c) Second order reaction:

$\quad\quad$ $2^{\text {nd }}$ order Reactions

$\quad\quad$ Two types

$\quad\quad$ $A+A \longrightarrow \text { products }$

$\quad\quad$ $a \quad a $

$\quad\quad$ $(a-x)(a-x) $

$\quad\quad$ $\therefore \frac{d x}{d t}=k(a-x)^{2} $

$\quad\quad$ $\Rightarrow \frac{1}{(a-x)}-\frac{1}{a}=k t $

$\quad\quad$ $A+B \longrightarrow \text { products. }$

$\quad\quad$ $ a \quad b $

$\quad\quad$ $a-x \quad b-x $

$\quad\quad$ $\frac{d x}{d t}=k(a-x)(b-x)$

$\quad\quad$ $ k=\frac{2.303}{t(a-b)} \log \frac{b(a-x)}{a(b-x)}$

METHODS TO DETERMINE ORDER OF A REACTION

(a) Initial rate method:

$$ r=k[A]^{\mathrm{a}}[\mathrm{B}]^{\mathrm{b}}[\mathrm{C}]^{\mathrm{c}} \quad \text { if } \quad[\mathrm{B}]=\text { constant } $$

$$ \quad \quad\quad\quad\quad\quad\quad\quad\quad\quad [C]=\text { constant } $$

then for two different initial concentrations of A we have

$r_{0_{1}} = k[A_0]_1^{a},$

$r_{0_{2}} = k[A_0]_2^{a}$

$\implies \frac{r_{0_1}}{r_{0_2}} = \big(\frac{[A_0]_1}{[A_0]_2}\big)^a$

(b) Using integrated rate law :

It is method of trial and error.

(c) Method of half lives :

for $\mathrm{n}^{\text {th }}$ order reaction $\quad t_{1 / 2} \propto \frac{1}{\left[R_{0}\right]^{n-1}}$

(d) Ostwald Isolation Method :

rate $=k[A]^{a}[B]^{b}[C]^{c}=k_{0}[A]^{a}$

METHODS TO MONITOR THE PROGRESS OF THE REACTION :

(a) Progress of gaseous reaction can be monitored by measuring total pressure at a fixed volume & temperature or by measuring total volume of mixture under constant pressure and temperature.

$\therefore \quad k = \frac{2.303}{t} log\frac{P_0(n-1)}{nP_0-P_t}$

{Formula is not applicable when $\mathrm{n}=1$, the value of $\mathrm{n}$ can be fractional also.}

(b) By titration method :

1.$\quad \therefore a \propto V_{0} \quad a-x \propto V_{t}$

$ k=\frac{2.303}{t} \log \frac{V_{0}}{V_{t}}$

2.Study of acid hydrolysis of an ester.

$k= \frac{2.303}{t}log\frac{V_{\infty}-V_0}{V_{\infty}-V_t}$

(c) By measuring optical rotation produced by the reaction mixture :

$k=\frac{2.303}{\mathrm{t}} \log \left(\frac{\theta_{0}-\theta_{\infty}}{\theta_{\mathrm{t}}-\theta_{\infty}}\right)$

EFFECT OF TEMPERATURE ON RATE OF REACTION

T.C. $=\frac{K_{t+10}}{K_t} \approx 2$ to 3 ( for most of the reactions)

Arrhenius theory of reaction rate

$E_P > E_r \rightarrow$ endothermic

$E_P < E_r \rightarrow$ exothermic

$\Delta H=\left(E_{p}-E_{r}\right)=$ enthalpy change

$\Delta H=E_{af}-E_{ab}$

$E_{threshold} = E_{af} + E_r = E_b + E_p$

Arrhenius equation

$ k = Ae^{-E_{a}RT} \quad r=k[conc.]^{order}$

$\frac{d ln k}{dT}=\frac{E_a}{RT^{2}}$

$\log k=(-\frac{Ea}{2.303 R}) \frac{1}T+\log A$

If $k_1 \quad and \quad k_2$ be the rate constant of a reaction at two different temperature $T_1 \quad and \quad T_2$ respectively, then we have

$$ \log \frac{k_{2}}{k_{1}}=\frac{E_{a}}{2.303 R} \left(\frac{1}{T_{1}}-\frac{1}{T_{2}}\right) $$

• lnk= ln $A-\frac{E_a}{RT}$

$\mathrm{E}_{\mathrm{a}} \geq \mathrm{O}$

• $\mathrm{T} \rightarrow \infty, \mathrm{K} \rightarrow \mathrm{A}.$