Capacitors:

(i) Capacitance Equation:

$$q \propto V \Rightarrow q = CV$$

• $q$: Charge on positive plate of the capacitor

• $C$: Capacitance of capacitor.

• $V$: Potential difference between positive and negative plates.

(ii) Representation of capacitor:

(iii) Energy stored in the capacitor:

$$U = \frac{1}{2} CV^2 = \frac{Q^2}{2C} = \frac{QV}{2}$$

(iv) Energy density

$$ \text{Energy density }= \frac{1}{2} \varepsilon_0 \varepsilon_r E^2 = \frac{1}{2} \varepsilon_0 KE^2$$

• $\varepsilon_r$: Relative permittivity of the medium.

• $K = \varepsilon_r$: Dielectric Constant

• For vacuum, energy density $= \frac{1}{2} \varepsilon_0 E^2$

(v) Types of Capacitors:

(a) Parallel plate capacitor

$$C = \frac{\varepsilon_0 \varepsilon_r A}{d} = K\frac{\varepsilon_0 A}{d}$$

• $A$: Area of plates

• $d$: distance between the plates ($\ll$ size of plate)

(b) Spherical Capacitor:

• Capacitance of an isolated spherical Conductor (hollow or solid)

$$C = 4 \pi \varepsilon_0 \varepsilon_r R$$

$R$: Radius of the spherical conductor

• Capacitance of spherical capacitor

$$C = 4 \pi \varepsilon_0 \frac{ab}{(b-a)} = \frac{4 \pi \varepsilon_0 K ab}{(b-a)}$$

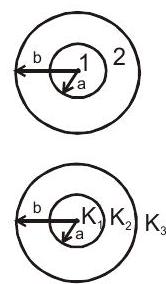
(c) Cylindrical Capacitor:

$\ell \gg {a, b}$

Capacitance per unit length: $$\frac{C}{l}= \frac{2 \pi \varepsilon_0}{\ell \ln(b / a)} \text{F/m}$$

(vi) Capacitance of capacitor depends on:

(a) Area of plates

(b) Distance between the plates

(c) Dielectric medium between the plates.

(vii) Electric field intensity between the plates of capacitor:

$$E = \frac{\sigma}{\varepsilon_0} = \frac{V}{d}$$

$\sigma$: Surface charge density

(viii) Force experienced by any plate of capacitor:

$$F = \frac{q^2}{2A\varepsilon_0}$$

Distribution of Charges on Connecting Two Charged Capacitors:

When two capacitors $C_1$ and $C_2$ are connected as shown in the figure:

(a) Common potential:

$$V = \frac{C_1 V_1 + C_2 V_2}{C_1 + C_2} = \frac{\text{Total charge}}{\text{Total capacitance}}$$

(b) Capacitance Equation:

$$Q_1’ = C_1 V = \frac{C_1}{C_1 + C_2}(Q_1 + Q_2)$$

$$Q_2’ = C_2 V = \frac{C_2}{C_1 + C_2}(Q_1 + Q_2)$$

(c) Heat loss during redistribution:

$$\Delta H = U_i - U_f = \frac{1}{2} \frac{C_1 C_2}{C_1 + C_2}(V_1 - V_2)^2$$

The loss of energy is in the form of Joule heating in the wire.

Combination of Capacitor

(i) Series Combination:

$$\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}$$

$$V_1 : V_2 : V_3 = \frac{1}{C_1} : \frac{1}{C_2} : \frac{1}{C_3}$$

(ii) Parallel Combination:

$$C_{eq} = C_1 + C_2 + C_3$$

$$Q_1 : Q_2 : Q_3 = C_1 : C_2 : C_3$$

Charging and Discharging of a Capacitor:

(i) Charging of Capacitor (Capacitor initially uncharged):

$$q = q_0(1 - e^{-t / \tau})$$

• $q_0$: Charge on the capacitor at steady state

• $q_0 = CV$

• $\tau$: Time constant $= CR_{eq}$

• Current: $$I = \frac{q_0}{\tau} e^{-t / \tau} = \frac{V}{R} e^{-t / \tau}$$

(ii) Discharging of Capacitor:

$$q = q_0 e^{-t / \tau}$$

• $q_0$: Initial charge on the capacitor

• Current: $$I = \frac{q_0}{\tau} e^{-t / \tau}$$

Capacitor with Dielectric:

(i) Capacitance in the presence of dielectric:

• Capacitance in the presence of dielectric: $$C = \frac{K \varepsilon_0 A}{d} = KC_0$$

• $C_0$: Capacitance in the absence of dielectric.

(ii) Inside A Dielectric Material:

$$E_{in} = E - E_{ind} = \frac{\sigma}{\varepsilon_0} - \frac{\sigma_b}{\varepsilon_0} = \frac{\sigma}{K\varepsilon_0} \frac{V}{d}$$

$E: \frac{\sigma}{\varepsilon_0}$: Electric field in the absence of dielectric

$E_{ind}$: Induced (bound) charge density.

(iii) Relationship Between Bound Charge Density And Free Charge Density

$$\sigma_b = \sigma\left(1 - \frac{1}{K}\right).$$

Force on Dielectric:

(i) When the battery is connected:

$$F = \frac{\varepsilon_0 b(K - 1)V^2}{2d}$$

(ii) When the battery is not connected:

$$F = \frac{Q^2}{2 C^2} \frac{dC}{dx}$$

(iii) The force on the dielectric will be zero when the dielectric is fully inside.