Electric Current:

• Average current: $I_{av} = \frac{\Delta q}{\Delta t}$

• Instantaneous current: $i = \lim_{\Delta t \to 0} \frac{\Delta q}{\Delta t} = \frac{dq}{dt}$

Electric Current in a Conductor:

$I = nAeV$ $v_d = \frac{\lambda}{\tau}$ $v_d = \frac{\frac{1}{2}\left(\frac{eE}{m}\right)\tau^2}{\tau} = \frac{1}{2} \frac{eE}{m} \tau$ $I = neAV_d$

Current Density:

$\vec{J} = \frac{dI}{dS} \vec{n}$

Electrical Resistance:

$I = neAV_d = neA\left(\frac{eE}{2m}\right)\tau = \left(\frac{ne^2 \tau}{2m}\right)AE$

$E = \frac{V}{\ell}$

so $I = \left(\frac{ne^2 \tau}{2m}\right)\left(\frac{A}{\ell}\right)V = \left(\frac{A}{\rho \ell}\right)V = \frac{V}{R} \Rightarrow V = IR$

Resistivity: $\rho = \frac{2m}{ne^2 \tau} = \frac{1}{\sigma},$

where $\sigma$ is conductivity.

Dependence of Resistance on Temperature: $R = R_0(1 + \alpha \theta).$

Electrical Power:

$P = VI$ $\text{Energy}= \int P dt$ $P = I^2R = VI = \frac{V^2}{R}$ $H = VIt = I^2Rt = \frac{V^2}{R}t$

Kirchhoff’s Laws:

Kirchhoff’s Current Law (Junction law): $\Sigma I_{in} = \Sigma I_{out}$

Kirchhoff’s Voltage Law (Loop law): $\Sigma IR + \Sigma \text{EMF} = 0.$

Combination of Resistances:

Resistances in Series: $R = R_1 + R_2 + R_3 + \ldots + R_n$

Resistances in Parallel: $\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$

Resistance of a Conductor:

The resistance $R$ of a conductor can be calculated using the formula: $R = \rho \frac{L}{A}$

Wheatstone Network:

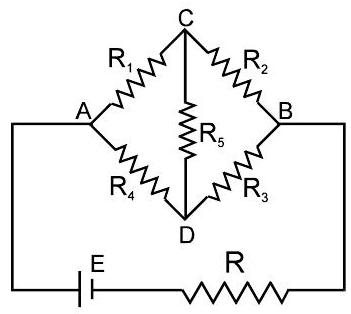
When current through the galvanometer is zero (null point or balance point), $\frac{P}{Q} = \frac{R}{S}$

Grouping of Cells:

• Cells in Series: Equivalent EMF $E_{eq} = E_1 + E_2 + \ldots + E_n$

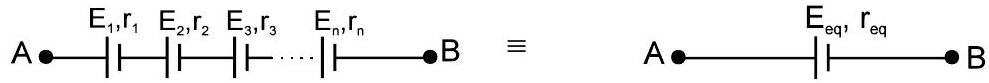
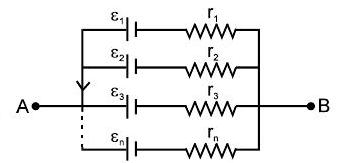
• Cells in Parallel: $E_{eq} = \frac{\varepsilon_1 / r_1 + \varepsilon_2 / r_2 + \ldots + \varepsilon_n / r_n}{1 / r_1 + 1 / r_2 + \ldots + 1 / r_n}$

Ammeter:

• A shunt (small resistance) is connected in parallel with a galvanometer to convert it into an ammeter.

• An ideal ammeter has zero resistance.

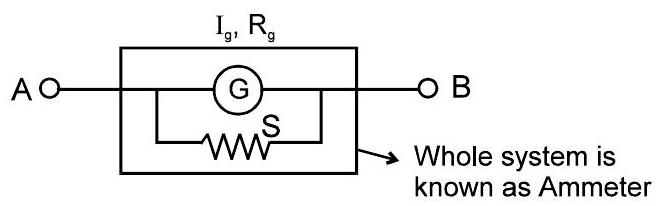
Ammeter is represented as follows -

If maximum value of current to be measured by ammeter is I then $I_{G} \cdot R_{G}=\left(I-I_{G}\right) S$

$S=\frac{I_{G} \cdot R_{G}}{I-I_{G}} \quad S=\frac{I_{G} \times R_{G}}{I} \quad when \quad I \gg I_{G.}$

where; $I=$ Maximum current that can be measured using the given ammeter.

Voltmeter:

• A high resistance is put in series with a galvanometer.

• It is used to measure the potential difference across a resistor in a circuit.

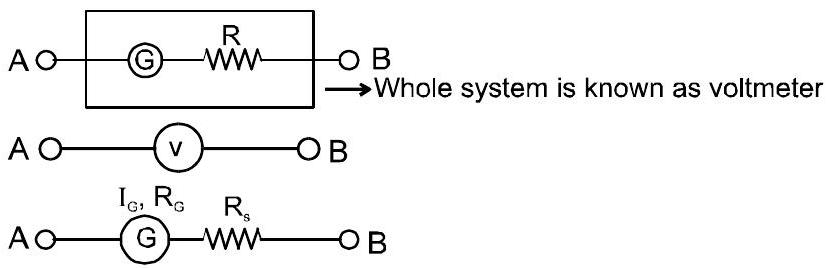
For maximum potential difference

$V = I_{G}.R_{S}+ I_{G}R_{G}$

$R_{S}=\frac{V}{I_{G}}-R_{G}$

$\text { if } \quad R_{G}«R_{S} \Rightarrow R_{S} \approx \frac{V}{I_{G}}$

Potentiometer:

Used for comparing EMFs, measuring internal resistance of cells, and calibrating ammeters and voltmeters.

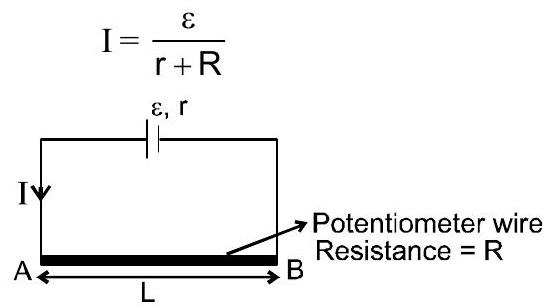
$V_{A}-V_{B}=\frac{\varepsilon}{R+r} \cdot R$

Potential gradient (x): Potential difference per unit length of wire

$x=\frac{V_{A}-V_{B}}{L}=\frac{\varepsilon}{R+r} \cdot \frac{R}{L}$

Application of potentiometer

(a)To find emf of unknown cell and compare emf of two cells.

In case I,

In figure (1) is joint to (2) then balance length $=\ell_{1} $

In case II,

$\varepsilon_{1}=x \ell_{1} \hspace{10mm}…(i)$

In figure (3) is joint to (2) then balance length $=\ell_{2}$

$\varepsilon_{2}=\mathrm{x} \ell_{2} \hspace{10mm}…(ii)$

$\frac{\varepsilon_{1}}{\varepsilon_{2}}=\frac{\ell_{1}}{\ell_{2}}$

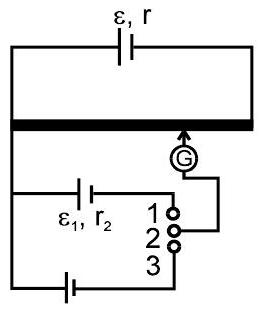
If any one of $\varepsilon_{1}$ or $\varepsilon_{2}$ is known the other can be found. If $\mathrm{x}$ is known then both $\varepsilon_{1}$ and $\varepsilon_{2}$ can be found

(b) To find current if resistance is known

$V_{A}-V_{C}=x \ell_{1}$

$R_{1}=x\ell_{1}$

$I=\frac{x \ell_{1}}{R_{1}}$

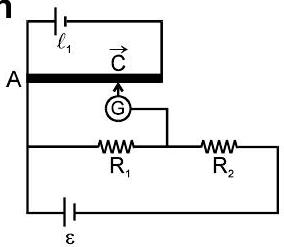
Similarly, we can find the value of $R_{2}$ also.

Potentiometer is ideal voltmeter because it does not draw any current from circuit, at the balance point.

(c) To find the internal resistance of cell.

Ist arrangement $\hspace{60mm}$ 2nd arrangement

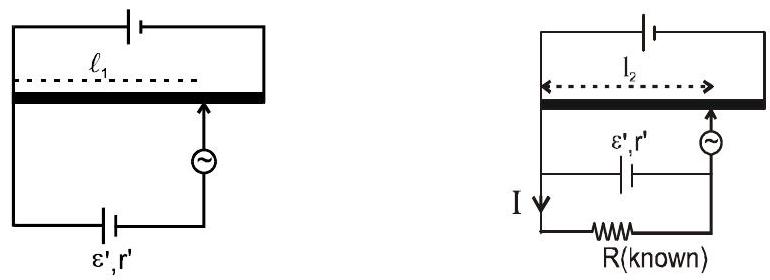
by first arrangement: $\varepsilon^{\prime}=\mathrm{x} \ell_{1} \hspace{10mm}…(i)$

by second arrangement: $\mathrm{IR}=\mathrm{x} \ell_{2}$

$I=\frac{\mathrm{x} \ell_{2}}{R}, \quad \text { also } I=\frac{\varepsilon^{\prime}}{r^{\prime}+R}$

$\therefore \quad \frac{\varepsilon^{\prime}}{r^{\prime}+R} = \frac{xl_{2}}{R} \quad \Rightarrow \frac{xl_{1}}{r^{\prime}+R} = \frac{xl_{2}}{R}$

$=\left[\frac{\ell_{1}-\ell_{2}}{\ell_{2}}\right] R$

(d) Ammeter and voltmeter can be graduated by potentiometer.

(e) Ammeter and voltmeter can be calibrated by potentiometer.

Metre Bridge:

Used to measure unknown resistance using the principle of a balanced Wheatstone bridge.

If $A B=\ell \mathrm{cm}$, then $B C=(100-\ell) \mathrm{cm}$.

Resistance of the wire between $A$ and $B, R \propto \ell$

[ $\because$ Specific resistance $\rho$ and cross-sectional area A are same for whole of the wire ]

$ \text { or } \quad R=\sigma \ell \hspace{10mm}…(i) $

where $\sigma$ is resistance per $\mathrm{cm}$ of wire.

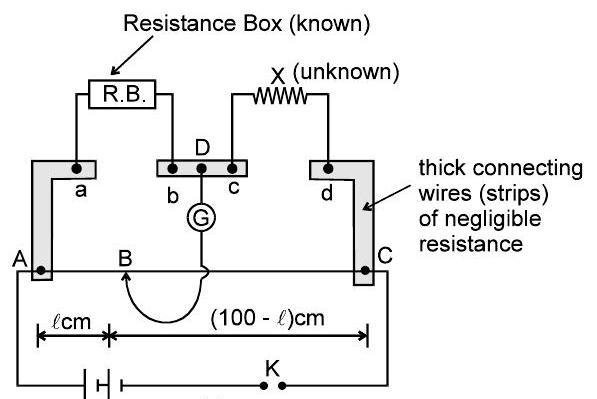
(a)

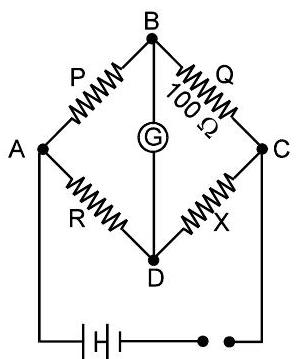
(b)

If $P$ is the resistance of wire between $A$ and $B$ then

$ P \propto \ell \Rightarrow \quad P=\sigma(\ell) $

Similarly, if $Q$ is resistance of the wire between $B$ and $C$, then

$ \begin{array}{ll} & Q \propto 100-\ell \ \therefore & Q=\sigma(100-\ell)\hspace{10mm}….(2) \end{array} $

Dividing (1) by (2), $ \frac{P}{Q}=\frac{\ell}{100-\ell}$

Applying the condition for balanced Wheatstone bridge, we get $R Q=P X$

$ \therefore \quad x=R \frac{Q}{P} \quad \text { or } \quad x=\frac{100-\ell}{\ell} R $

Since $\mathrm{R}$ and $\ell$ are known, therefore, the value of $\mathrm{X}$ can be calculated.

Ohm’s law:

$ V = I R $