Average Velocity (in an interval) :

$$ v_{av} = \overline{v} = \langle v \rangle = \frac{ \text{Total displacement}}{\text{ Total time taken}} = \frac{\vec{\mathrm{x_f}} - \vec{\mathrm{x_i}}}{\Delta t} $$

Average Velocity For n Velocities:

$$\frac{1}{v_{av}}= \frac{1}{v_1} +\frac{1}{v_2} +…+ \frac{1}{v_n}$$

Average Speed (in an interval):

$$\text{Average Speed} =\frac{ \text{Total distance travelled} }{ \text{ Total time taken }}$$

Instantaneous Velocity (at an instant) :

$$\vec{\mathrm{v}}_{\mathrm{inst}}=\lim _{\Delta \mathrm{t} \rightarrow 0}\left(\frac{\Delta \vec{\mathrm{x}}}{\Delta \mathrm{t}}\right)$$

Average Acceleration (in an interval):

$$v_{av} = \frac{\Delta \vec{v}}{\Delta t} = \frac{\vec{v_f} - \vec{v_i}}{\Delta t}$$

Instantaneous Acceleration (at an instant):

$$\vec{a}=\frac{d \vec{v}}{d t}=\lim _{\Delta t \rightarrow 0}\left(\frac{\vec{\Delta v}}{\Delta t}\right)$$

Graphs in Uniformly Accelerated Motion along a straight line $(a \neq 0)$:

• $x$ is a quadratic polynomial in terms of $t$. Hence $x-t$ graph is a parabola.

x-t graph

v-t graph

• $v$ is a linear polynomial in terms of $t$. Hence $v-t$ graph is a straight line of slope a.

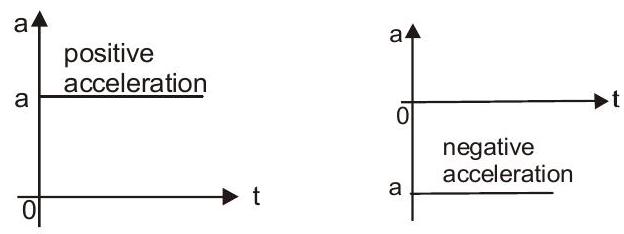
a-t graph

• a-t graph is a horizontal line because a is constant.

Maxima & Minima

• At maximum: $$\frac{dy}{dx} = 0,\quad \frac{d}{dx}\left(\frac{dy}{dx}\right)<0 $$

• At minima: $$\frac{dy}{dx} = 0,\quad \frac{d}{dx}\left(\frac{dy}{dx}\right)>0 $$

Equations of Motion (for constant acceleration):

,

(a) $ v=u+a t$

(b) $s=u t+\frac{1}{2}a t^{2} \quad s=v t-\frac{1}{2}a t^{2} \quad x_{f}=x_{i}+u t+\frac{1}{2} a t^{2}$

(c) $ v^{2}=u^{2}+2 a s$

(d) $\mathrm{s}=\frac{(\mathrm{u}+\mathrm{v})}{2} \mathrm{t}$

(e) $s_{n}=u+\frac{a}{2}(2 n-1)$

For freely falling bodies: $u = 0$

(taking upward direction as positive)

(a) $\mathrm{v}=-\mathrm{gt}$

(b) $\mathrm{s}=\frac{1}{2} \mathrm{gt}^{2} \hspace{10mm}\mathrm{s}=\mathrm{vt}+\frac{1}{2} \mathrm{gt}^{2} \hspace{10mm}h_{f}=h_{i}-\frac{1}{2} g t^{2}$

(c) $v^{2}=2 g s$

(d) $\quad s_{n}=-\frac{g}{2}(2 n-1)$