Chapter 10 Wave Optics
Exercises
10.1 Monochromatic light of wavelength $589 \mathrm{~nm}$ is incident from air on a water surface. What are the wavelength, frequency and speed of
(a) reflected, and (b) refracted light? Refractive index of water is 1.33 .
Show Answer
Answer
Let $I_{1}$ and $I_{2}$ be the intensity of the two light waves. Their resultant intensities can be obtained as:
$I^{\prime}=I_{1}+I_{2}+2 \sqrt{I_{1} I_{2}} \cos \phi$
Where,
$\phi=$ Phase difference between the two waves
For monochromatic light waves,
$$ \begin{aligned} & I_{1}=I_{2} \\ & \begin{aligned} \therefore I^{\prime} & =I_{1}+I_{1}+2 \sqrt{I_{1} I_{1}} \cos \phi \\ & =2 I_{1}+2 I_{1} \cos \phi \end{aligned} \end{aligned} $$
Phase difference $=\frac{2 \pi}{\lambda} \times$ Path difference
Since path difference $=\lambda$,
Phase difference, $\phi=2 \pi$
$\therefore I^{\prime}=2 I_{1}+2 I_{1}=4 I_{1}$
Given,
$I^{\prime}=K$
$\therefore I_{1}=\frac{K}{4}$
When path difference $=\frac{\lambda}{3}$,
Phase difference, $\phi=\frac{2 \pi}{3}$
Hence, resultant intensity, $I_{R}^{\prime}=I_{1}+I_{1}+2 \sqrt{I_{1} I_{1}} \cos \frac{2 \pi}{3}$
$=2 I_{1}+2 I_{1}\left(-\frac{1}{2}\right)=I_{1}$
Using equation (1), we can write:
$I_{R}=I_{1}=\frac{K}{4}$
Hence, the intensity of light at a point where the path difference is $\frac{\lambda}{3}$ is $\frac{K}{4}$ units.
10.2 What is the shape of the wavefront in each of the following cases:
(a) Light diverging from a point source.
(b) Light emerging out of a convex lens when a point source is placed at its focus.
(c) The portion of the wavefront of light from a distant star intercepted by the Earth.
Show Answer
Answer
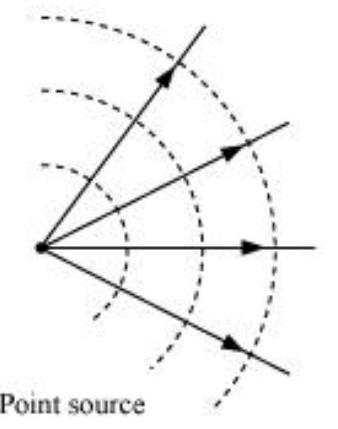
The shape of the wavefront in case of a light diverging from a point source is spherical. The wavefront emanating from a point source is shown in the given figure.
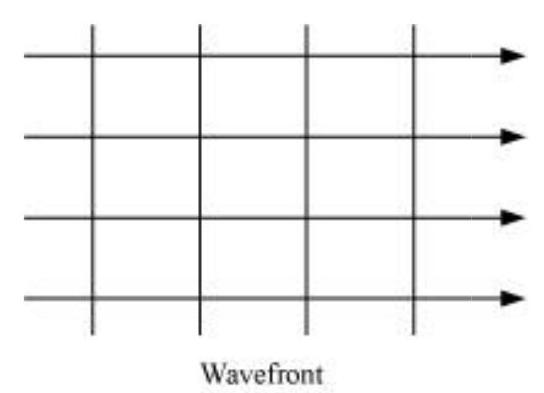
The shape of the wavefront in case of a light emerging out of a convex lens when a point source is placed at its focus is a parallel grid. This is shown in the given figure.
The portion of the wavefront of light from a distant star intercepted by the Earth is a plane.
10.3 (a) The refractive index of glass is 1.5 . What is the speed of light in glass? (Speed of light in vacuum is $3.0 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}$)
(b) Is the speed of light in glass independent of the colour of light? If not, which of the two colours red and violet travels slower in a glass prism?
Show Answer
Answer Refractive index of glass, $\mu=1.5$
Speed of light, $\mathrm{c}=3 \times 10^{8} \mathrm{~m} / \mathrm{s}$
Speed of light in glass is given by the relation,
$$ \begin{aligned} v & =\frac{c}{\mu} \\ & =\frac{3 \times 10^{8}}{1.5}=2 \times 10^{8} \mathrm{~m} / \mathrm{s} \end{aligned} $$
Hence, the speed of light in glass is $2 \times 10^{8} \mathrm{~m} / \mathrm{s}$.
The speed of light in glass is not independent of the colour of light.
The refractive index of a violet component of white light is greater than the refractive index of a red component. Hence, the speed of violet light is less than the speed of red light in glass. Hence, violet light travels slower than red light in a glass prism.
10.4 In a Young’s double-slit experiment, the slits are separated by $0.28 \mathrm{~mm}$ and the screen is placed $1.4 \mathrm{~m}$ away. The distance between the central bright fringe and the fourth bright fringe is measured to be $1.2 \mathrm{~cm}$. Determine the wavelength of light used in the experiment.
Show Answer
Answer
Distance between the slits, $d=0.28 \mathrm{~mm}=0.28 \times 10^{-3} \mathrm{~m}$
Distance between the slits and the screen, $D=1.4 \mathrm{~m}$
Distance between the central fringe and the fourth $(n=4)$ fringe,
$u=1.2 \mathrm{~cm}=1.2 \times 10^{-2} \mathrm{~m}$
In case of a constructive interference, we have the relation for the distance between the two fringes as:
$u=n \lambda \frac{D}{d}$
Where,
$n=$ Order of fringes $=4$ $\lambda=$ Wavelength of light used
$$ \therefore=\frac{u d}{n D} $$
$=\frac{1.2 \times 10^{-2} \times 0.28 \times 10^{-3}}{4 \times 1.4}$
$=6 \times 10^{-7}$
$=600 \mathrm{~nm}$
Hence, the wavelength of the light is $600 \mathrm{~nm}$.
10.5 In Young’s double-slit experiment using monochromatic light of wavelength $\lambda$, the intensity of light at a point on the screen where path difference is $\lambda$, is $K$ units. What is the intensity of light at a point where path difference is $\lambda / 3$ ?
Show Answer
Answer
Let $I_{1}$ and $I_{2}$ be the intensity of the two light waves. Their resultant intensities can be obtained as:
$I^{\prime}=I_{1}+I_{2}+2 \sqrt{I_{1} I_{2}} \cos \phi$
Where,
$\phi=$ Phase difference between the two waves
For monochromatic light waves,
$$ \begin{aligned} & I_{1}=I_{2} \\ & \begin{aligned} \therefore I^{\prime} & =I_{1}+I_{1}+2 \sqrt{I_{1} I_{1}} \cos \phi \\ & =2 I_{1}+2 I_{1} \cos \phi \end{aligned} \end{aligned} $$
Phase difference $=\frac{2 \pi}{\lambda} \times$ Path difference
Since path difference $=\lambda$,
Phase difference, $\phi=2 \pi$
$\therefore I^{\prime}=2 I_{1}+2 I_{1}=4 I_{1}$
Given,
$I^{\prime}=K$
$\therefore I_{1}=\frac{K}{4}$
When path difference $=\frac{\lambda}{3}$,
Phase difference, $\phi=\frac{2 \pi}{3}$
Hence, resultant intensity, $I_{R}^{\prime}=I_{1}+I_{1}+2 \sqrt{I_{1} I_{1}} \cos \frac{2 \pi}{3}$
$=2 I_{1}+2 I_{1}\left(-\frac{1}{2}\right)=I_{1}$
Using equation (1), we can write:
$I_{R}=I_{1}=\frac{K}{4}$
Hence, the intensity of light at a point where the path difference is $\frac{\lambda}{3}$ is $\frac{K}{4}$ units.
10.6 A beam of light consisting of two wavelengths, $650 \mathrm{~nm}$ and $520 \mathrm{~nm}$, is used to obtain interference fringes in a Young’s double-slit experiment.
(a) Find the distance of the third bright fringe on the screen from the central maximum for wavelength $650 \mathrm{~nm}$.
(b) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?
Show Answer
Answer
Wavelength of the light beam, $\lambda_{1}=650 \mathrm{~nm}$
Wavelength of another light beam, $\lambda_{2}=520 \mathrm{~nm}$
Distance of the slits from the screen $=D$
Distance between the two slits $=d$
Distance of the $n^{\text {th }}$ bright fringe on the screen from the central maximum is given by the relation,
$x=n \lambda_{1}\left(\frac{D}{d}\right)$
For third bright fringe, $n=3$
$\therefore x=3 \times 650 \frac{D}{d}=1950\left(\frac{D}{d}\right) \mathrm{nm}$
Let the $n^{\text {th }}$ bright fringe due to wavelength $\lambda_{2}$ and $(n-1)^{\text {th }}$ bright fringe due to wavelength $\lambda_{1}$ coincide on the screen. We can equate the conditions for bright fringes as:
$$ \begin{aligned} & n \lambda_{2}=(n-1) \lambda_{1} \\ & 520 n=650 n-650 \\ & 650=130 n \\ & \therefore n=5 \end{aligned} $$
Hence, the least distance from the central maximum can be obtained by the relation:
$$ \begin{aligned} x & =n \lambda_{2} \frac{D}{d} \\ & =5 \times 520 \frac{D}{d}=2600 \frac{D}{d} \mathrm{~nm} \end{aligned} $$
Note: The value of $d$ and $D$ are not given in the question.





